[역학] 역학기초 - 단면1,2차 모멘트 / 단면계수

내가 공부하려고 정리하는 역학
문제를 풀다보면 단면1차/2차 모멘트랑 단면계수를 풀어야 할 때가 많다.
간단한 도형의 기본식을 외우는것이 좋을 듯 하다.

[출처]
개인 정리 + 위키백과 + 구조역학특강자료 (신현길 강사님)

1.
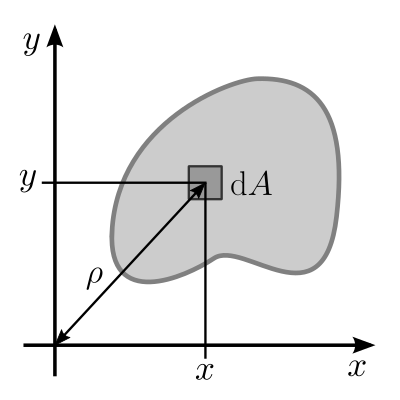
단면 1차 모멘트 (G : 기하학 모멘트)

: x,y 축으로부터 도심점까지의 거리에 면적을 곱한 것.
: 단위는 거리*미소면적이므로 세제곱이 붙음 (ex. m3 / cm3)
: 도심 G를 지나는 축에 대한 단면 1차 모멘트는 반드시 0 이다. (거리가 0이므로)
: 합성단면의 단면 1차 모멘트는 두 도형의 단면 1차 모멘트 각각의 합과 같다.
: +,- 부호가 있다.

2.
단면 2차 모멘트 ( I : 극관성 모멘트)

: 휨응력(f)에 대한 견고성을 표시하는 단면계수(Z)를 구하기 위함
: 단위는 거리의 제곱 * 미소면적 이므로 네제곱이 붙는다. (ex. m4/cm4)
: 도심축에 대한 단면2차 모멘트는 최소이다. (0은아님)
: 정방형(정사각형, 정원형단면)의 단면 2차 모멘트는 축의 회전에 관계없이 일정하다.
: 무조건 +(양)이다.

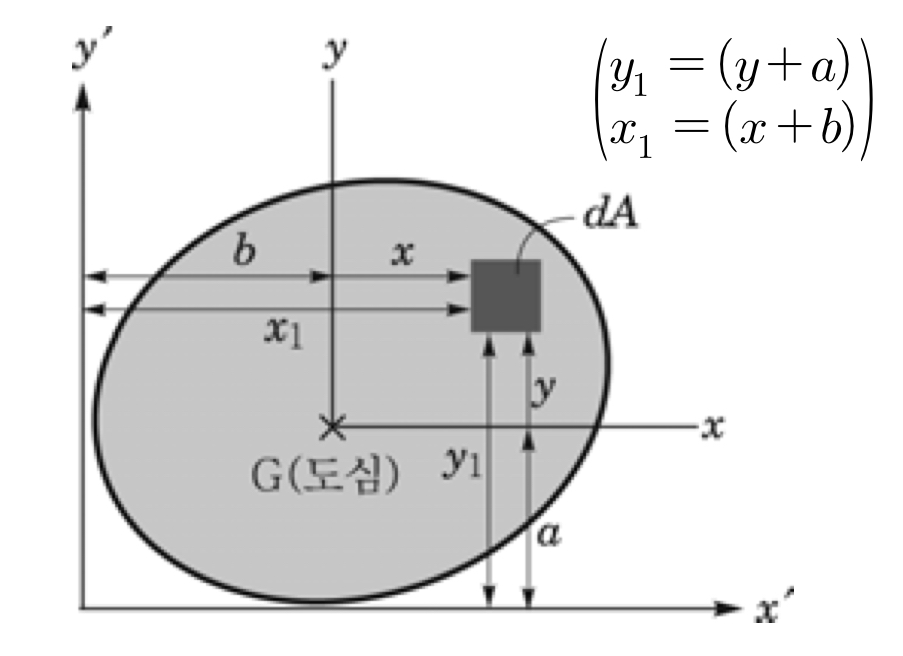
: 평행축 공식 암기 필요

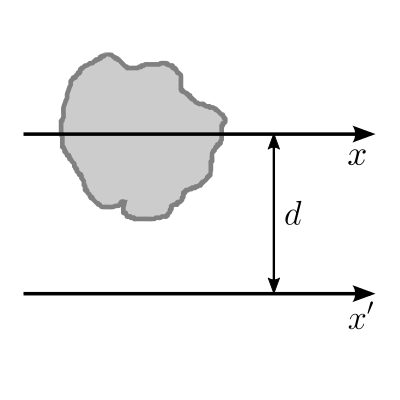
중립축과 평행한 임의의 축 (x’)에 대한 단면 2차 모멘트 공식 암기 필요

Ix’ = Ix + Ad ²
(Ix’ : x’축에 대한 단면2차 모멘트
Ix : x축에 대한 단면 2차 모멘트
A : 단면의 넓이 / d : x축과 x’축 사이의 거리)

3.
단면계수 (Z)

: 보의 굽힘강도를 측정하는데 사용된다. (휨에 대한 견고성)
: 단면 2차 모멘트를 단면의 가장 끝단에서 도심까지의 거리로 나눈 값

4.
주요 단면의 수식